Harmonie a 4 související pojmy
Rovnováha, harmonie a soulad
Rovnováha (balanc) je pojem, který se používáme pro stavy ve stylu 50 : 50. Avšak harmonie nemusí mít na každé straně stejnou hodnotu (!), nicméně příslušný systém musí sladěně (!) fungovat – jako například pravá a levá ruka. Základním symbolem rovnováhy v rámci Jednoty je monáda – znak harmonického spojení protikladů známý jako jing-jang:  Základním cvičením harmonie, respektive pro rovnováhu (zvláště tělesnou) je cvičení (resp. postoj) Volavka, přičemž je ještě psychická verze pojmu volavka (dole v odkazovaném příspěvku).
Základním cvičením harmonie, respektive pro rovnováhu (zvláště tělesnou) je cvičení (resp. postoj) Volavka, přičemž je ještě psychická verze pojmu volavka (dole v odkazovaném příspěvku).
Též viz článek „Co dělat, když se nemůžete rozhodnout? Vyzkoušejte pravidlo 10 / 10 / 10!“ . A asi viz vše vyhledatelné na to téma: https://www.google.com/search?q=pot%C3%AD%C5%BEe+se+rozhodnout.
„ Soulad (vnější harmonie) nepropaguje sebe, nýbrž tvoření lepšího světa skrze každého z nás. Pomáhá, aby to dobré v sobě objevil každý sám. Léčivé místo uvnitř sebe stvořené k ztišení mysli a zklidnění těla, k procítění své přirozenosti, přírody a všeho živého.
S láskou a pokorou ke všemu a všem.
#soulad “ – citováno z https://www.soulad.cz/?v=928568b84963.

Tensegrity a soudržnost (harmonie) Všehomíra
S pojmem tensegrity jsem se poprvé setkal při čtení o architektonickém výtvoru, jehož vzletný vzhled (typu harmonie) mne zaujal. Byla to myslím stavba držená ocelovými lanky a vzepjetím vnitřní konstrukce (přepjatá ocel?).

Tensegrity je tedy vlastně harmonický (protože NAPJATĚ rovnovážný) stav. Můj odborný názor je, že do psychické verze tohoto pojmu patří i vzrušení a vzrušování.
Další zajímavou souvislostí je Jóga.
Kořenem toho pojmu je slovo „jóg“ (anglicky „yog“) což v sanskrtu (nejstarší a svatý jazyk) znamená soudržnost panující ve Všehomíru. Jak však můžeme vidět, příslušná soudržnost (viz i základní známé 4 síly) je tak-nějak napjatá (jako tensegrity vysvětlená výše).
Z kvantové fyziky se postupně vynořuje pátá (poslední) síla (interakce). Jde o okamžité vzájemné ovlivňování (propletené kvantové stavy)…: „
Nechť jsou vyzářeny dva elektrony. Ať je tato dvojice částic vyzářena s celkovým momentem hybnosti nulovým. Pak musíme díky zákonu zachování momentu hybnosti při libovolném pozorování tohoto systému vždy zjistit celkový moment hybnosti dvojice elektronů nulový.
Elektron má velikost spinu polovinu Planckovy konstanty a může mít jen dvě projekce spinu vůči danému směru plus nebo mínus polovina Planckovy konstanty (jinak řečeno projekce nahoru nebo dolů). Pokud tedy naměříme projekci spinu do daného směru u jednoho elektronu kladnou, u druhého musíme ve stejném směru naměřit zápornou. Pro každý z dvojice elektronů není projekce spinu definována.
Společná vlnová funkce je superpozicí dvou stavů. V prvním má první elektron projekci spinu kladnou a druhý zápornou a v druhém je tomu naopak. Kvadrát této vlnové funkce určuje pravděpodobnost, se kterou zjistíme konkrétní projekci u některého z nich. Jaký stav určíme v každém konkrétním měření u daného elektronu nelze říci. Když však změříme konkrétní projekci spinu u jedné částice, je pak stav druhé přesně a okamžitě definován, ať je v době měření jakkoliv daleko. Dochází k tomu už zmiňovanému kolapsu vlnové funkce.
V předchozím odstavci je popsána situace, která se označuje jako EPR paradox (paradox Einsteina, Podolského a Rosena). V daném případě v úpravě, kterou navrhl David Bohm. Albert Einstein, Boris Podolský a Nathan Rosen předpokládali lokálnost a argumentovali, že musí existovat nějaké „skryté“ parametry. Ty by měly již při vyzáření elektronů určovat, který z elektronů bude mít spin nahoru a který dolů. Jinak by se musela informace mezi objekty propleteného stavu přenášet nadsvětelnou rychlostí. Druhou možností, kterou obhajoval Niels Bohr, bylo smíření se s už zmíněnou nelokálností kvantové fyziky.
Lze nelokálnost kvantové fyziky potvrdit?
Rozhodnutí o tom, jestli existují skryté parametry, které sice nedokážeme pozorovat, ale definují naměřené veličiny už při vzniku stavu, nebo je kvantová fyzika nelokální, přinesl experiment navržený Johnem S. Bellem. Ten spočíval zase v měření projekce spinu dvojice elektronů do různých směrů pootočených o nějaký úhel ϑ. Podíváme se tedy na projekci spinu u prvního elektronu do nějakého směru a druhého elektronu na projekci do směru o zmíněný úhel pootočeného. Výsledek měření bude u obou elektronů vždy buď nahoru, nebo dolů.
Pokud budou hodnoty projekce do daného směru u prvního elektronu i u druhého projekce do směru pootočeného o zmíněný úhel ϑ obě stejné (buď obě nahoru, nebo obě dolů), dostaneme korelaci a přiřadíme tomuto měření jedničku.
Když budou opačné (dostaneme antikorelaci) přiřadíme mu mínus jedničku. Pokud změříme pro každý úhel spoustu případů a uděláme ze získaných sérií mínus a plus jedniček střední hodnotu, dostaneme v závislosti na úhlu ϑ různé hodnoty v intervalu mezi -1 až +1. O této veličině budeme mluvit jako o míře korelace pro dané nastavení směrů projekce spinů.
Například pro ϑ = 0o dostaneme čistou hodnotu -1, jde o případ, který jsme popsali výše a pro který ze zákona zachování momentu hybnosti plyne, že projekce spinu jednotlivých elektronů musí být opačná a jde tedy o úplnou antikorelaci.
Ze stejných důvodů bude úplná korelace a námi určovaná střední hodnota +1 pro úhel 180o. V případě, kdy je úhel 90o nebo 270o jsou vybrané směry projekce u jednotlivých elektronů na sebe kolmé. Protože lze vždy určit jen projekci spinu pouze do jednoho směru, nezávisí v tomto případě nijak výsledek měření u druhého elektronu na výsledku u prvního. Bude tak stejná pravděpodobnost dostat pro naši korelační veličinu hodnotu +1 i -1 a střední hodnota při velkém počtu měření, kdy dostaneme stejný počet plus i mínus jedniček, tak bude nula.
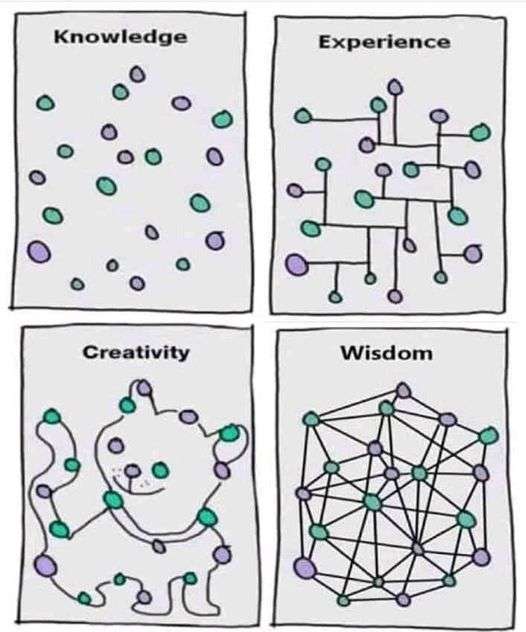
Tomu bude stejně v případě platnosti nelokální kvantová teorie i v případě existence skrytých parametrů, které už na počátku definují, jak měření dopadnou. Ovšem pro úhly, které jsou mezi těmito hodnotami, to už bude jiné, tam se budou střední hodnoty námi sledované korelační veličiny v případě existence skrytých parametrů a nelokálnosti lišit. Střední hodnota sledované veličiny korelace bude v případě existence skrytých parametrů vždy mezi nulou a hodnotou na modré lomené křivce v obrázku.
V případě platnosti nelokálnosti kvantového světa bude tato hodnota přesně dána červenou goniometrickou funkcí v obrázku.
Je vidět, že pro dané úhly nemohou hodnoty míry korelace v případě lokálnosti a existence skrytých parametrů překročit určité meze. To je obsahem tzv. Bellových nerovností. Při správném nastavení experimentu je naměření větší absolutní hodnoty míry korelace důkazem, že opravdu platí nelokální kvantová teorie. Zvětšit obrázek
Závislost míry korelace na úhlu mezi směry, do kterých probíhá projekce spinu dvou částic se spinem 1/2, které vznikly společně a jsou v propleteném stavu. Modrá lomená křivka ukazuje maximální hodnotu míry korelace v případě lokálnosti a existence skrytých parametrů. Červená pak přesnou hodnotu v případě platnosti nelokální kvantové fyziky.
Při reálných experimentálních testech, zda jsou u propletených kvantových systémů splněny Bellových nerovností, se nejčastěji pracuje s fotony a jejich polarizací. Než se k nim dostaneme, budeme se v následujících pár odstavcích věnovat upřesněním některých pojmů souvisejících s polarizací zvláště elektromagnetického záření a fotonů.
Pro další čtení není tato část nezbytně nutná. Pokud čtenář příslušné pojmy zná nebo bez dalšího vysvětlení příjme fakt, že jak světlo, tak i jednotlivý foton můžou být polarizovány, můžou „kmitat“ v některém směru kolmém na směr jejich šíření, tak lze následující část přeskočit.
Spin, helicita a polarizace fotonu
Význačným směrem, do kterého bude probíhat projekce spinu, může být směr pohybu příslušné částice. Orientace projekce spinu tak může být ve směru pohybu (hybnosti) dané částice nebo proti směru. V takovém případě mluvíme o helicitě. Její hodnota může být +1 v případě, že projekce spinu je orientována stejně jako směr pohybu (mluvíme také o pravotočivé helicitě) nebo -1 v případě, že projekce spinu je orientována opačně než směr pohybu (levotočivá helicita).
Je třeba poznamenat, že helicita závisí na vzájemném pohybu pozorovatele a pozorované částice. Jestliže pozorujeme částici s pravotočivou helicitou (tedy +1) a posléze se začneme pohybovat ve směru pohybu tato částice rychleji než ona, tak se směr jejího pohybu vůči nám otočí, ale projekce spinu do směru zůstává stejná. Pravotočivá helicita částice se změní na levotočivou. Pochopitelně se v tomto případě změní levotočivá helicita částice na pravotočivou.
Řekli jsme si, že v případě spinu 1/2 jsou možné dvě projekce spinu a tedy dvě možné hodnoty helicity. V případě částice se spinem 1 jsou možné tři projekce spinu -1, 0 a +1. A také tři možné hodnoty helicity -1, 0, +1. Tato situace nastává například u deuteronu. V případě, že však částice má nulovou klidovou hmotnost, což je případ fotonu, jsou možné jen dvě projekce spinu do osy pohybu částice -1 a +1, tedy i jen dvě možné hodnoty helicity.
U takových částic je ještě jedna specifická vlastnost, pohybují se rychlostí světla, takže pozorovatel nemůže zrychlit na rychlost větší. Helicita daného fotonu je tak pro každého pozorovatele stejná. Počet projekcí spinu NS s jeho rostoucí velikostí roste a lze je určit ze vztahu NS=2S+1, kde S je velikost spinu. U helicity už tomu tak není, Tam jsou stále dvě možné hodnoty v případě poločíselného spinu a tři hodnoty pro celočíselný spin (dvě hodnoty v případě částic s nulovou klidovou hmotností).
Fotony jsou částicemi světla a helicita je na mikroskopické úrovni podstatou polarizace.
Pro levotočivou či pravotočivou helicitu máme příslušnou kruhovou polarizaci. Eliptická či lineární polarizace se pak dostane příslušnou superpozicí levotočivé a pravotočivé kruhové polarizace. A tato superpozice popisuje jednotlivý foton s lineární polarizací. P
opsané vlastnosti fotonů stojí i za makroskopickou polarizaci světla. V tomto případě jde o kmitání elektrického pole kolmo na směr pohybu světla, které udržuje stejný směr. Nepolarizované světlo kmitá také kolmo na směr pohybu světla ale do různých směrů. Pochopitelně můžeme dostat i pro makroskopické světlo kromě lineární i kruhovou či eliptickou polarizaci.
Výsledky experimentů testujících nelokálnost kvantové fyzikyPrvní experimenty, které testovaly Bellovy nerovnosti, využívaly fotony s korelovanými polarizacemi vyzářenými ve vybrané kaskádě za sebou při následujících přechodech elektronů v obalu atomu vápníku. Proud atomů vápníku byl ozařován lasery a pomocí nich byly elektrony vybuzeny do daných stavů s vyšší energií. Přebytečné energie se atom zbavoval tak, že elektron nejdříve přeskočil do stavu s nižší energií. Přitom se vyzáří první foton. A z tohoto mezistavu téměř okamžitě přeskočí do základního stavu s vyzářením dalšího fotonu.
Protože původní a vybuzený stav mají moment hybnosti nula a mezistav má nenulový moment hybnosti, klade zákon zachování momentu hybnosti jistá omezení na vztah polarizace jednotlivých fotonů ve vyzářené dvojici. Situace je tak velice podobná situaci dvojice elektronů, kterou jsme popisovali dříve. Dostáváme tak dvojici fotonů v propleteném stavu s korelovanými polarizacemi.
Pro zjišťování polarizace fotonů se využívaly i ve známé práci Alaina Aspecta v Orsay tzv. Wollastonovy polarizační hranoly složené ze dvou kusů islandského vápence. Ty vlastně určovaly směr projekce, podobně jako v dřívějším popisu propletené dvojice elektronů.
Rozdíl je v tom, že v případě lineární polarizace definuje polarizace se směrem šíření světla rovinu.
Při otočení polarimetru o 45o dostaneme nekorelované případy a při jeho otočení o 90o antikorelaci, při otočení polarimetru o 180o máme stejnou situaci jako na počátku. Pokud se podíváme na obrázek se zobrazením míry korelace na úhlu, který byl uveden v diskuzi elektronového páru, tak sice platí i pro případ studia Bellových nerovností pomocí polarizace fotonů.
Ovšem úhel na ose x je v tomto případě dvojnásobkem úhlu mezi nastaveními dvou použitých polarizačních hranolů. V průběhu experimentu se dělalo vše pro to, aby nastavení polarizačního hranolu v jednom rameni (kam letěl první foton) neovlivňovalo situaci v druhém rameni, kam letěl ten druhý nebo dokonce proces vyzáření nějakou klasickou cestou.
Proto se hranoly nastavovaly až po vyzáření fotonů. U těchto experimentů, které probíhaly na rozhraní sedmdesátých a osmdesátých let, byla vzdálenost mezi zdrojem fotonů v propleteném stavu a polarizačními hranoly šest metrů. Tuto vzdálenost uletí světlo za 20 ns. Výsledky měření se shodovaly s předpovědí nelokální kvantové mechaniky a vyloučily lokální teorii se skrytými parametry. Tím se prokázalo, že kvantový stav představuje úplný popis reality a že neurčitosti, které v popisu jsou, jsou objektivní a nejsou důsledkem našich neznalostí.
„ – citováno z https://www.osel.cz/5110-podivnosti-kvantoveho-sveta.html.
Inkluze
Inkluze (zařazení *slabšího*) v českém školství je v současné době poměrně problém… Zatím se to řeší s pomocí asistentů – a to už vypadá (překvapivě?) „průchodně“, nicméně (nadměrně) nákladně. Jak byste to zharmonizoval(a) Vy?
Invalidé mají vlastní olympiádu (= paralympiáda) a o jejich inkluzi mezi standardní sportovce jistě nikdo normální neuvažuje. Na příslušném principu považujeme zvláštní školy za vhodnější vyřešení vzdělávání pro podprůměrně inteligentní či jinak problematické děti. Tím více vítáme třídy pro nadané děti! Jednoduše řečeno, lidé nejsou stejní.
Nejlepší by byl podle nás prakticky opak inkluze, čili aby se různě nadané děti vyučovali vzhledem ke svým vlohám! Současný stupidní systém školství v České republice i jinde ve světě (kromě pár výjimek jako je pro příklad Finsko) vypadá následovně.

Více viz (anglicky)..: The Education System: “Now Climb That Tree” | The Marquette Educator (wordpress.com), (1) Why Teach Squirrels To Swim or Ducks To Climb Trees ? | LinkedIn atd.